Radial keratotomy (RK) is no longer performed to treat myopia. Surgeons, however, still face the challenges that prior RK presents to cataract surgery and, specifically, to IOL power calculations. Many RK procedures were performed in the 1980s and early ‘90s on patients who were then in their 20s or 30s. For this reason, a steady stream of these patients will present for cataract surgery in the coming years.
COMPARING METHODS
RK is distinct from laser vision correction with regard to its effects on biometry and IOL calculations (see Challenges of Biometry and IOL Calculations After Radial Keratotomy). Post-LASIK formulas therefore should not be applied to post-RK eyes. It is also unusual for patients to recall or have a record of their pre-RK refractions.
Challenges of Biometry and IOL Calculations After RK
1. The relationship between anterior and posterior curvature is altered but differently and to a lesser degree than after laser vision correction.
2. The optical zone is small (often < 3.00 mm), so keratometers usually measure outside the flattened central zone and overestimate corneal power.
3. Topography is irregular.
4. Corneal instability after radial keratotomy results in diurnal variations in refraction and progressive hyperopia over time.
5. Corneal instability can cause a hyperopic shift soon after cataract surgery, followed by myopic regression.
6. Axial length is often higher than average, rendering many formulas for IOL calculation less accurate.
7. Keratometry is abnormally flat, rendering many formulas for IOL calculation less accurate.
8. Patient dependence on contact lenses may make it difficult for them to discontinue lens wear long enough to improve the accuracy of biometry.
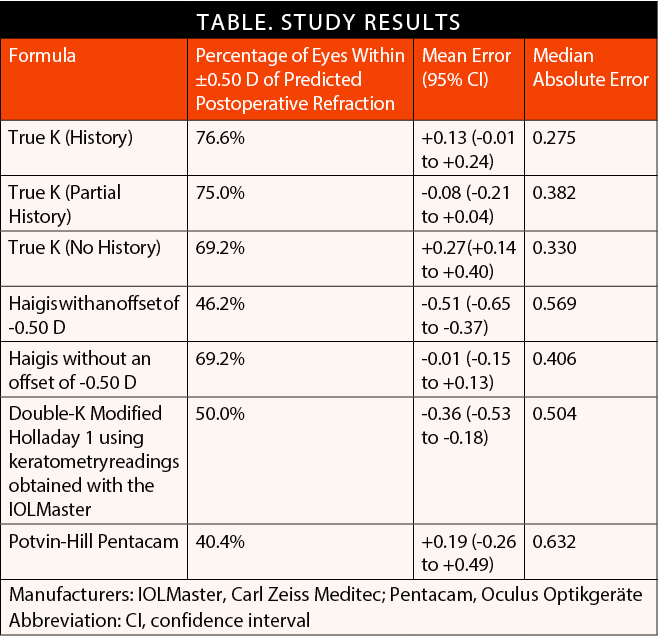
My colleagues and I recently compared seven methods of IOL calculation after previous RK.1 These included three options for the RK algorithm of the True K formula, which underwent a significant update in 2016 (version 2.5), two formulas from the ASCRS calculator (the Potvin-Hill Pentacam [Oculus Optikgeräte] and the double-K modified Holladay 1 using keratometry readings obtained with the IOLMaster [Carl Zeiss Meditec]), and the standard Haigis formula, both with and without an offset of -0.50 D.
Methodology. Our analysis was conducted on a dataset of 34 patients (52 eyes), all of whom underwent cataract surgery at the same institution where they had undergone RK several years earlier (Lions Eye Institute, Perth, Australia). For this reason, a complete refractive history predating RK was available for almost all of the patients. This unique advantage enabled us to make a robust comparison of IOL formulas, some of which require elements of the refractive history. All of the cataract procedures were performed by a single surgeon (Graham D. Barrett, MD, FRANZCO), and patients received either model SN60WF or SN6ATx of the AcrySof IQ lens (Alcon). A subjective refraction was obtained 4 to 6 weeks postoperatively. None of the eyes in this dataset had been previously used to derive the True K formula.
Results. The lowest median absolute error (MAE, 0.275) and highest percentage (76.6%) of eyes within ±0.50 D of the predicted postoperative refraction were achieved with the True K formula using both the pre- and post-RK refraction data (True K [History]), with a mean error (ME) of +0.13 (95% CI, -0.01 to +0.24).
Interestingly and importantly, omitting the pre-RK data and including only the post-RK refraction (True K [Partial History]) was associated with only a modest reduction in accuracy (MAE of 0.382 and 75% of eyes within ±0.50 D of target) and with actually a more favorable, low myopic ME of -0.08 (95% CI, -0.21 to +0.04). With neither pre- nor post-RK data (True K [No History]), 69.2% of eyes were within ±0.50 D of target, and MAE was 0.330. There was a greater tendency, however, toward hyperopic surprises, with an ME of +0.27 (95% CI, +0.14 to +0.40).
The concept of the post-RK refraction deserves further explanation. After RK, corneal curvature tends to flatten over time, leading to a gradual hyperopic drift that may be quite extreme in some cases. This is often partially counteracted by index myopia from nuclear sclerosis. The key with the post-RK refraction is to try to identify the most hyperopic refraction on record for a patient (ie, to allow the maximum hyperopic drift before the cataract developed).
Unlike the hyperopic and myopic LASIK algorithms of the True K formula, which use the refractive history only when data from both before and after laser treatment are entered, the RK algorithm has been modified to allow just the post-RK data to be used, even when the pre-RK refraction box is left blank (calc.apacrs.org/Barrett_True_K_Universal_2105).
Given that the True K (History) and True K (Partial History) were the most accurate of the methods analyzed and had similar efficacy, there is a clear value to obtaining and entering at least the post-RK refractive data. The nature of the post-RK refraction means that it should be readily available in most instances because it does not require accessing records from many years ago. Adding the pre-RK data offers a small additional benefit, and they should be used when available.
In patients for whom no refractive history was available, the True K (No History) performed similarly to the standard Haigis formula (with no offset) in terms of the percentage of patients within ±0.50 D of their refractive target. The Haigis formula returned an ME closer to emmetropia and with fewer hyperopic surprises than the True K (No History), but the MAE was higher (0.406 vs 0.330). The efficacy of the Haigis formula in this context is explained by the fact that it does not rely on keratometry to predict the effective lens position. This enables the formula to perform reasonably well in eyes with abnormal corneas.
The other formulas investigated were found to be less accurate than the True K options or the Haigis formula. The double-K modified Holladay 1 using keratometry readings obtained with the IOLMaster produced an MAE of 0.504, and only 50% of eyes achieved a result within ±0.50 D of target. This method also erred more on the side of myopia, with an ME of -0.36 (95% CI, -0.53 to -0.18). The Potvin-Hill Pentacam formula was the least accurate, with an MAE of 0.632, an ME of +0.19 (95% CI, -0.26 to +0.49), and only 40.4% of eyes achieving a result within ±0.50 D of target. These results are broken down in the Table below.
CONCLUSION
The updated algorithm of the True K formula provided greater accuracy than cataract surgeons were previously able to offer to patients with a history of RK. Refractive outcomes remained more variable, however, in this population than in virgin eyes. Patients should be made aware of this and of the greater surgical complexity posed by RK incisions, and they should be counseled that they will likely experience fluctuations in vision after cataract surgery.
Consideration should be given to the degree of irregular astigmatism and whether patients will still require contact lenses after surgery, in which case it may be prudent to avoid implanting toric IOLs.
1. Turnbull AMJ, Crawford GJ, Barrett GD. Methods for intraocular lens power calculation in cataract surgery after radial keratotomy. Ophthalmology. 2020;127(1):45-51.



